割り算の計算ができる人なら簡単に計算できます。
ルカ・パチョーリの７２法則を使います。
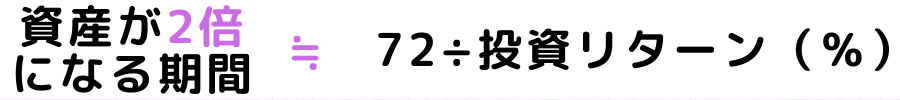
早速具体例で説明します。
- ケース①：年間の投資リターンを１％と仮定した場合⇒72÷1＝72、つまり約72年で資産が2倍になる！
- ケース②：年間の投資リターンを2％と仮定した場合⇒72÷2＝36、つまり約36年で資産が2倍になる！
- ケース③：年間の投資リターンを8％と仮定した場合⇒72÷8＝9、つまり約9年で資産が2倍になる！
- ケース④：年間の投資リターンを9％と仮定した場合⇒72÷9＝8、つまり約8年で資産が2倍になる！
計算自体は単純です。
投資リターンは現時点では誰にもわかりませんが、自分が投資している金融商品が将来どれだけのリターンを期待できるか、あるいは期待しているかによって計算式に代入する数字が変わることになります。
式と数字だけではピンとこないと思います。これをグラフ化してみました。
投資リターンによる違いは？
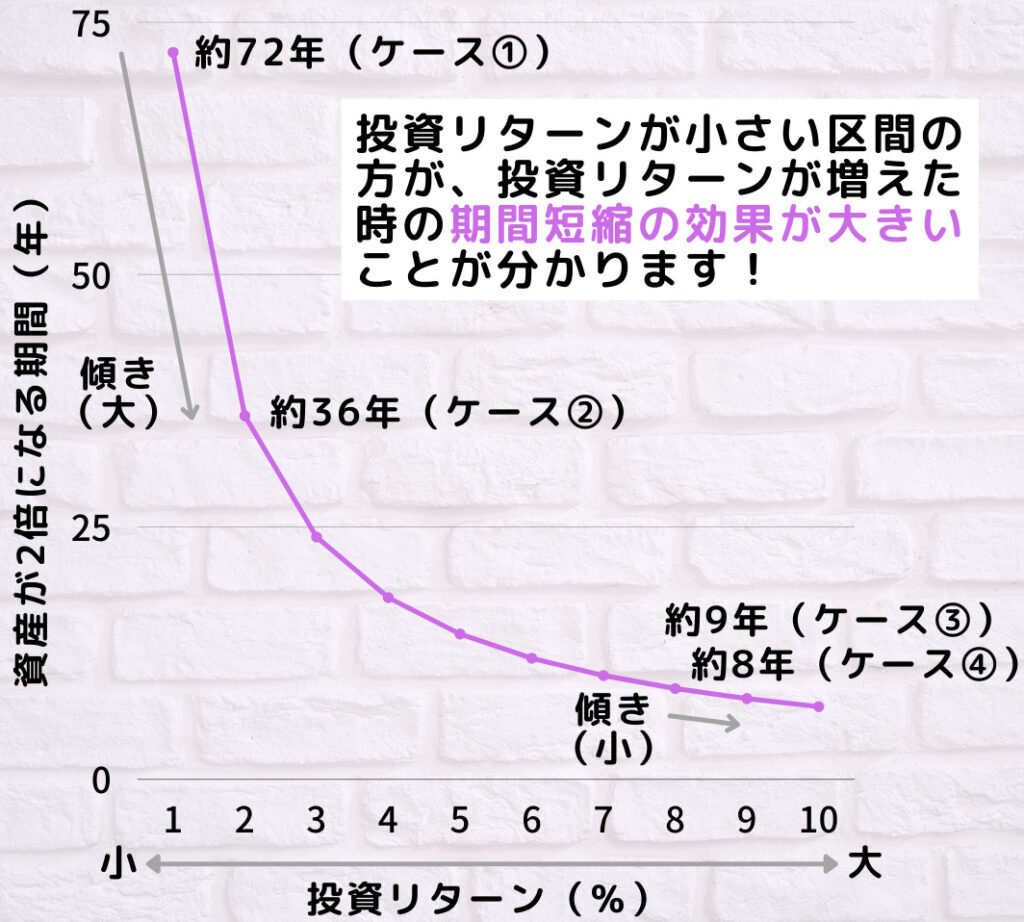
投資リターンが大きいケース③からケース④のように、そのリターンが１％大きくなっても、投資リターンが小さいケース①からケース②に比べると、資産が2倍になる期間の短縮効果は小さいと言えます。
一般的に、投資リターンが大きい金融商品はリスクが大きいと言われているので、投資リターンの大きさを追求する前に、このグラフを思い出すのも良いかもしれません。
７２の法則の計算精度は？
７２の法則を用いると非常に簡単な計算式で計算することができましたが、この式の計算結果って妥当なのでしょうか？
気になったので、正しい計算方法で検証してみました。
こちらが正しい計算式です。
Logの計算が含まれるので少し式が複雑です。
早速フラグ化してみました。
紫色のグラフが７２の法則で算出したフラフで、青色のグラフが正しい計算式で算出したグラフです。
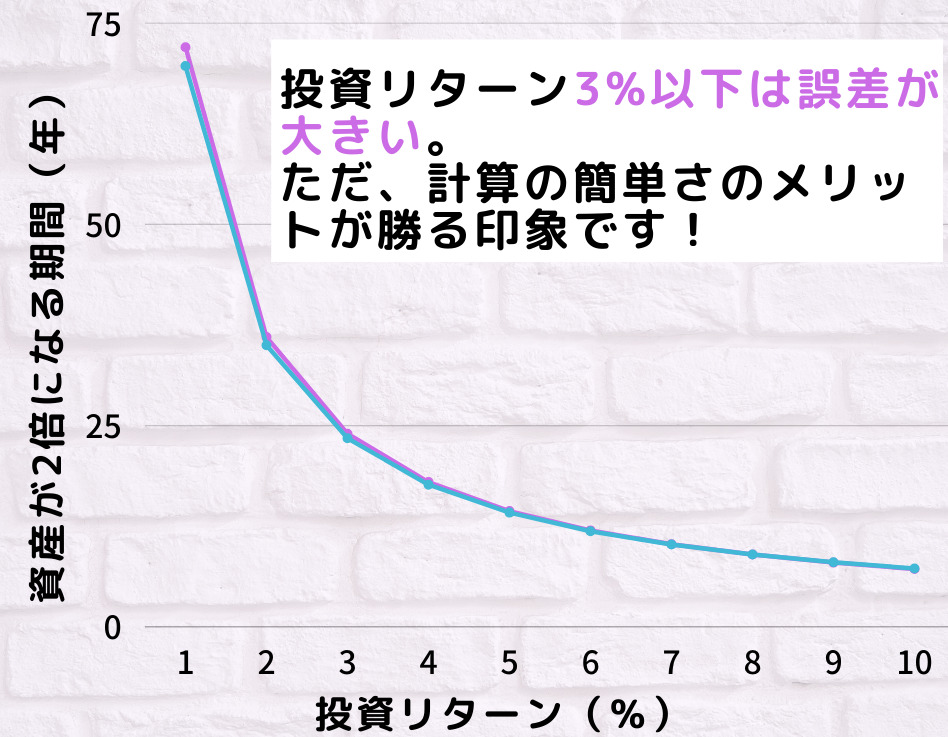
どちらのグラフも同じようなカーブを描くことが分かりました。
また、各投資リターンごとにそれぞれの式で算出した値を比較した結果、投資リターンが３％以下の場合は、計算結果の誤差が大きいものの、投資リターン４％〜10%の範囲では誤差は非常に小さいため、７２の法則は非常に有用な式であると思います。
銀行に預けた場合、資産が２倍になる期間は？
参考として、銀行の普通預金や定期預金に預けた場合について検証してみました。
金利（利息）については、時期によって異なるのであくまで参考値と思って下さい。
ただし、金利のオーダー（桁数）が急に変わるものでもないと思っています。
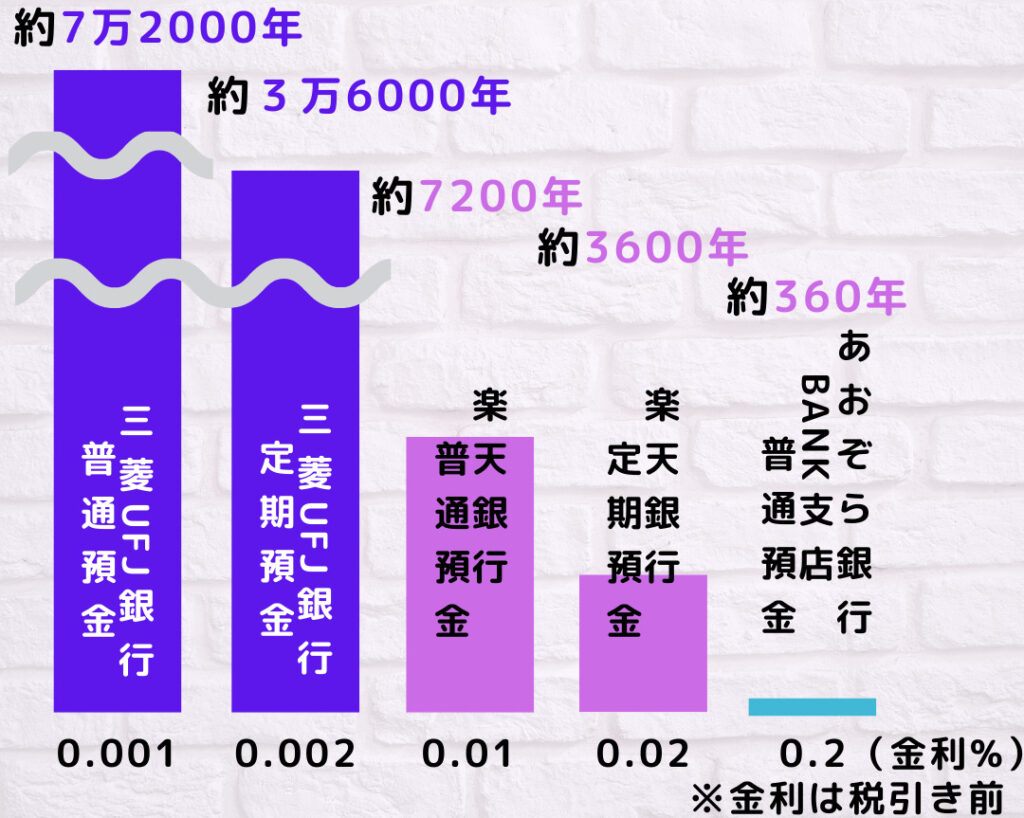
銀行にお金を預けても全く増えないことが、分かると思います。。
